Matières
Applications mobiles
Découvrir
© 2025 Astra.si. Tous droits réservés
"Pour la prochaine génération."
© 2025 Astra.si. Tous droits réservés
"Pour la prochaine génération."
Les fonctions trigonométriques sont des fonctions d'un angle. Elles permettent de faire le lien entre les angles et les longueurs des côtés d'un triangle, ou entre les angles et les coordonnées d'un point sur un cercle. Les fonctions de base sont le sinus (sin), le cosinus (cos), la tangente (tan) et la cotangente (cot). Elles sont fondamentales pour analyser tout phénomène périodique (qui se répète), comme les ondes ou les vibrations.
La manière la plus simple de définir ces fonctions est dans un triangle rectangle, pour un angle aigu a :
sin(a) = cote oppose / hypotenusecos(a) = cote adjacent / hypotenusetan(a) = cote oppose / cote adjacentcot(a) = cote adjacent / cote opposeCette définition est le point de départ, mais elle est limitée aux angles entre 0° et 90°. Pour généraliser, on utilise le cercle trigonométrique.
Le cercle trigonométrique est un cercle de rayon 1 centré sur l'origine d'un repère. C'est l'outil le plus puissant pour comprendre les fonctions trigonométriques pour n'importe quel angle.
Pour un angle a, on lui associe un point unique sur le cercle. Les coordonnées de ce point sont tout simplement (cos(a), sin(a)).
À partir de là, on définit la tangente et la cotangente :
tan(a) = sin(a) / cos(a) (n'est pas définie si cos(a) = 0)cot(a) = cos(a) / sin(a) (n'est pas définie si sin(a) = 0)sin(a + 2pi) = sin(a) et cos(a + 2pi) = cos(a). Le motif se répète tous les 360°.cos(-a) = cos(a). Sa courbe est symétrique par rapport à l'axe des ordonnées.sin(-a) = -sin(a). Sa courbe est symétrique par rapport à l'origine.C'est la formule la plus importante, issue directement du théorème de Pythagore dans le cercle trigonométrique : sin^2(a) + cos^2(a) = 1
Pour certains angles clés, les valeurs sont connues et très utilisées :
a = pi/6 (30°) : sin(a) = 1/2 et cos(a) = sqrt(3)/2a = pi/4 (45°) : sin(a) = sqrt(2)/2 et cos(a) = sqrt(2)/2a = pi/3 (60°) : sin(a) = sqrt(3)/2 et cos(a) = 1/2En conclusion, les fonctions trigonométriques sont les piliers de l'analyse des angles et des phénomènes périodiques. Leurs propriétés, définies par le cercle trigonométrique et régies par des identités clés, en font des outils incontournables en sciences et en ingénierie.
Qu'est-ce que la Trigonométrie ?
Explication
3 minutes
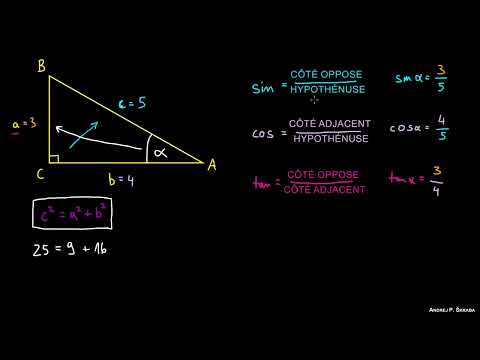
Les Bases des Fonctions Trigonométriques
Explication
9 minutes
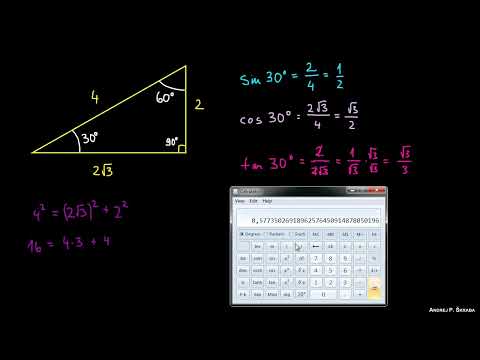
Exemple de Calcul avec les Fonctions Trigonométriques
Explication
10 minutes

Identités Trigonométriques
Explication
8 minutes
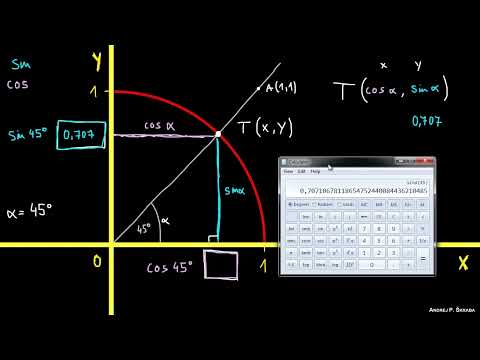
Sinus et Cosinus
Explication
11 minutes
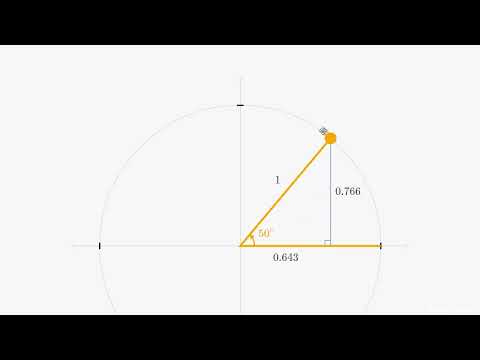
Tableau des Fonctions Trigonométriques
Explication
9 minutes

Comment Calculer un Angle avec la Trigonométrie
Explication
6 minutes

Simplifier les Expressions Trigonométriques
Explication
2 minutes
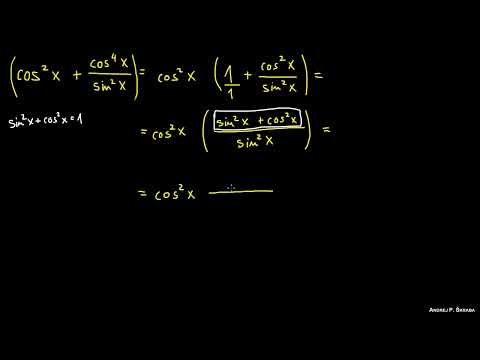
Stratégies de Simplification Trigonométrique
Explication
4 minutes