Matières
Applications mobiles
Découvrir
© 2025 Astra.si. Tous droits réservés
"Pour la prochaine génération."
© 2025 Astra.si. Tous droits réservés
"Pour la prochaine génération."
En analyse mathématique, l'un des concepts clés est celui qui décrit la variation d'une fonction par rapport à la variation de son argument. Ce concept mène à la définition formelle de la dérivée, qui est le fondement de nombreuses constructions et théories mathématiques ultérieures. L'idée centrale est que la dérivée mesure le taux de variation d'une fonction en un point donné – c'est-à-dire, à quelle vitesse et dans quelle direction la fonction change à cet endroit.
Soit 'f' une fonction réelle et x₀ un point de son domaine de définition. La dérivée de la fonction 'f' au point x₀ est notée f′(x₀) et est définie comme la limite du taux d'accroissement, si cette limite existe :
f′(x₀) = lim (quand h → 0) [f(x₀ + h) – f(x₀)] / h
Dans cette expression, 'h' représente une petite variation de la variable indépendante x, tandis que le numérateur montre la variation de la valeur de la fonction. Si cette limite existe, on dit que la fonction est dérivable en ce point.
Géométriquement, la dérivée représente la pente de la droite tangente au graphique de la fonction au point x₀. Si nous imaginons le graphique de la fonction comme une courbe lisse, alors la tangente en un point donné indique la direction dans laquelle la courbe se dirige. Plus la dérivée est grande, plus cette pente est raide.
Utilisons la définition :
f′(x) = lim (quand h → 0) [(x + h)² – x²] / h = lim (quand h → 0) [x² + 2xh + h² – x²] / h = lim (quand h → 0) [2xh + h²] / h = lim (quand h → 0) (2x + h) = 2x
Par conséquent, la dérivée de la fonction x² est 2x. Cela signifie que les valeurs de cette fonction au point x changent à un taux de 2x.
La dérivée est un outil mathématique pour décrire le taux de variation d'une fonction. En utilisant la limite du taux d'accroissement, nous arrivons à une définition précise qui a une signification à la fois numérique et géométrique. En comprenant des exemples de base, comme la fonction quadratique, nous pouvons plus facilement construire des connaissances sur des fonctions plus complexes.
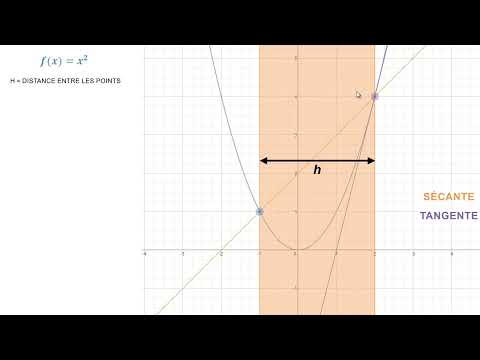
Qu'est-ce qu'une Dérivée ?
Explication
13 minutes
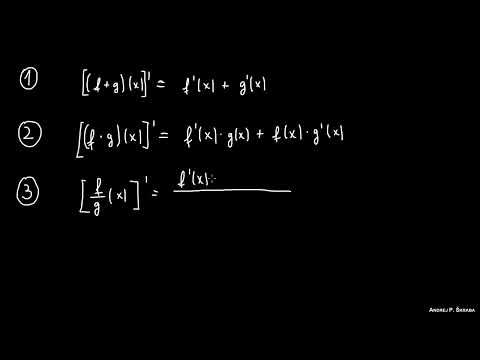
Les Règles de Dérivation
Explication
4 minutes

Règles de Calcul de la Dérivée
Explication
5 minutes

La Dérivée par la Définition 1
Explication
6 minutes
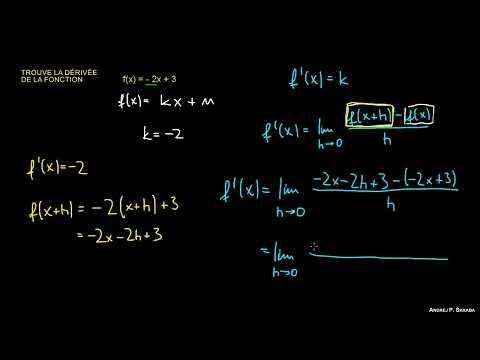
La Dérivée par la Définition 2
Explication
5 minutes
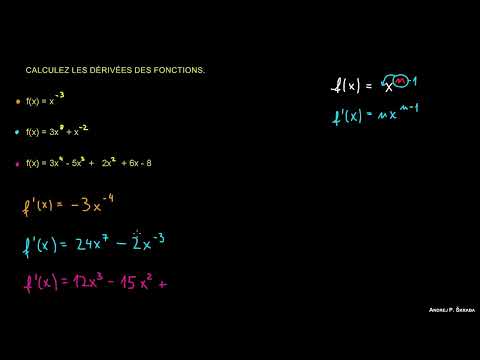
Dérivé – Exercice 1
Explication
5 minutes

Dérivé – Exercice 2
Explication
4 minutes

Dérivé – Exercice 3
Explication
4 minutes